BM25 Score
TF-IDF의 upgrade version, BM25 Score에 대해 정리합니다.
BM25
- TF-IDF 계열의 알고리즘이며, 좀 더 advanced version으로 SOTA 달성. (Elastic Search 에서도 활용)
- 쿼리에 포함되는 단어들이 특정 문서에서만 얼마나 더 자주 등장하는지 파악, 문서 별 유사도를 파악한다. (TF-IDF 와 목적은 동일하다.)
- TF IDF 단점
- 문서의 길이를 반영하여 계산하지 못한다. 그저 term frequency 즉, 문서에 존재 여부만 봄
-
score(D, Q) = sum (IDF(qi) * advanced_term_freduqncy(qi, D))

- tfNorm (advanced term frequency)
=(freq(qi, D) * (k1 + 1)) / (freq(qi, D) + k1 * (1 - b + b * |D|/avgdl))- 분자 ; $freq(q_i, D) * (k_1+1)$
- $k_1$
- term frequency 의 satuaration 을 결정하는 요소이다. (1.2 ~ 2.0 사이값이 일반적)
- $k_1$의 값이 작을수록, 단어의 빈도가 자주 등장할 때 bm25 score 에 미치는 영향은 작아진다.
- 주로 1.2 또는 2를 사용
- Example
- freq = 1, k1=1.2 인 경우 (1 - b(1 - |D| / avgdl) = C = 1 이라고 가정)
1 * (1.2 +1) / 1 + 1.2*C = 2.2 / 2.2 = 1 - freq = 10, k1=1.2 인 경우 (1 - b(1 - |D| / avgdl) = C = 1 이라고 가정)
10 * (1.2 + 1) / 10 + 1.2*C = 22 / 11.2 = 1.96
- freq = 1, k1=1.2 인 경우 (1 - b(1 - |D| / avgdl) = C = 1 이라고 가정)
- 즉, 만약 특정 단어가 term freq 가 높더라도, 값이 상승하는 증가 기울기에 영향을 미침.특정 freq 까지는 빠르게 증가하다가, 어느 정도의 freq를 만족한 이후에는 천천히 증가함
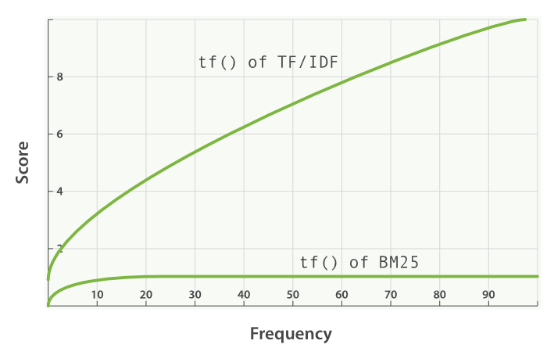
- term frequency 의 satuaration 을 결정하는 요소이다. (1.2 ~ 2.0 사이값이 일반적)
- $k_1$
-
분모 ; $freq(q_i, D) + k_1 * (1 - b + b*\frac{ D }{avgdl})$ -
$(1 - b + b*\frac{ D }{avgdl} )$ - IF 문서의 길이가 평균보다 크면, -> 이 term 이 1보다 커지게 되고 -> 분모에 있으므로 bm25 score가 작아지는 penalty를 받게 된다.
- IF 문서의 길이가 평균보다 짧으면, -> 분모 term 이 작아지고 -> bm25 score는 더 커지는 수혜를 입는다.
- IF 문서의 길이가 평균보다 크면, -> 이 term 이 1보다 커지게 되고 -> 분모에 있으므로 bm25 score가 작아지는 penalty를 받게 된다.
- 매우 긴 문서에서 동일한 단어가 등장하는 것보다, 짧은 문장에서 해당 단어가 등장할 때 더 큰 가중치를 주게 된다.
-
- 분자 ; $freq(q_i, D) * (k_1+1)$
- Inverse Document Frequency
=ln ( 1 + (len(docs) - freq(q_i, D) + 0.5 ) / freq(q_i, D) + 0.5 )- document frequency 의 역수격
타 문서에 자주 등장하는 token에 대해서 penalty를 주고자 함
- i.e “the” 라는 token을 자주 등장한다고 해서 의미있다고 보기 어려움.
10개의 문서에서 10번 모두 등장하면 => 0.05
10개의 문서에서 1번 등장하면 => 1.99
- i.e “the” 라는 token을 자주 등장한다고 해서 의미있다고 보기 어려움.
- DF 가 클수록, 이 값이 거의 0에 가깝게 수렴함 -> 불용어 영향 제거

- document frequency 의 역수격
타 문서에 자주 등장하는 token에 대해서 penalty를 주고자 함
- tfNorm (advanced term frequency)
- TF-IDF 대비 더 나은 성능을 보이는 이유
- 문서의 길이를 반영하는 term을 활용함. 문서의 길이가 평균대비 길면 penalty
- k1 saturation 을 활용하여, 점점 빈번해지더라도 score 상승 기울기를 조절함
- IDF term에서 DF 가 클수록 0에 가깝게 수렴 -> 불용어의 영향을 미비하게 만들 수 있음
Reference
- https://velog.io/@jkl133/BM25
- https://velog.io/@mayhan/Elasticsearch-%EC%9C%A0%EC%82%AC%EB%8F%84-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98