Elements of probability

  • sample space
  • set of outcomes
  • probability measures
    • event 가 입력으로 들어왔을 떄 거기에 대응되는 함수
  • 몇몇 properites

Random Variables

  • Probability Measure for Random Variable
    • CDF
      • culmulative
    • PMF (Mass Function)
      • discrete 한 경우
    • PDF (Density Function)
      • continuous 한 경우
      • density function 의 prob 자체는 매우 큰 무한대까지 가질 수 있음. 왜냐면, x의 범위가 어어어어엄청 0에 가깝게 작아지면, 적분하면 1이 되어야 해서.
      • 어떤 RV x 에서 어떤 RV y 에 대한 분포를 transformation 해서 구한다고 생각해보자.
        y = f(x) 일 때, P_y(y) = P_x(x)*|gradient| 로 구해짐.
        일반적으로 vector의 경우도 그러함. 여기서 f를 NN 으로 쓰게 되면, invertible 하지 않기 때문에 y의 likelihood 를 구할 수가 없음.
      • Normalizing Flow
        img
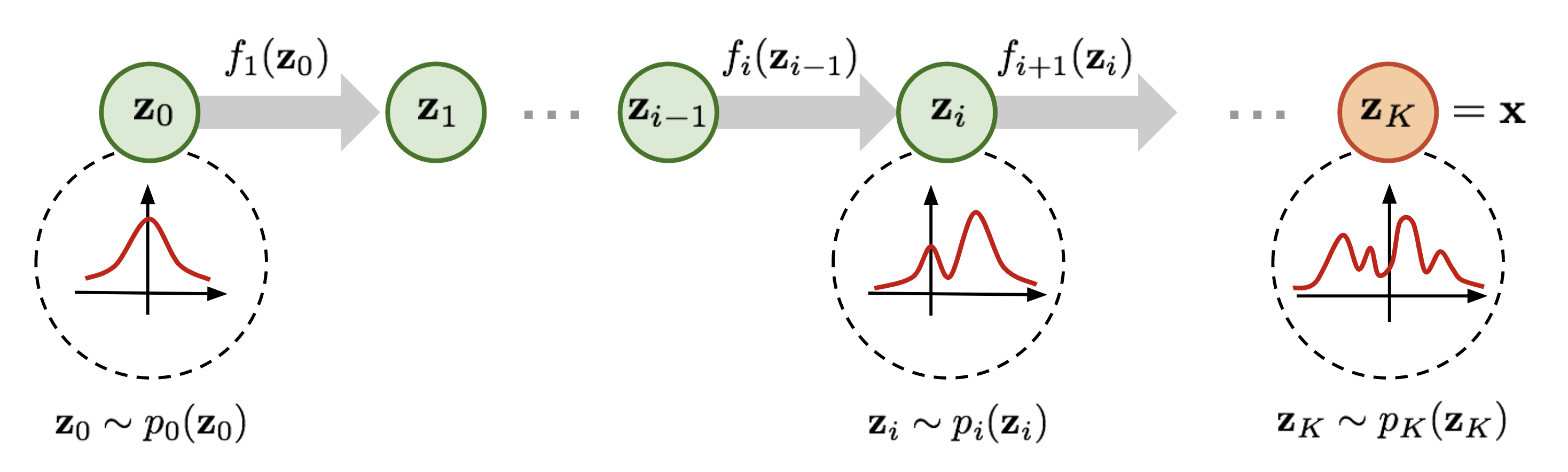
        Normalizing Flwo는 invertible transformation 을 통해 점점 좀 더 복잡한 distritbuiton 을 invertible한 연산을 통해 만들어 나간다.
        이를 통해 최종 target variable의 probability distribution을 invertible transformation을 통해 추적할 수 있다.
      • Masked Autoregressive Flow
        img
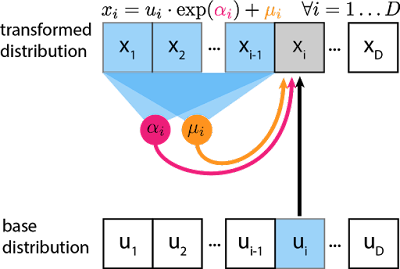
        각 step을 거치며 지나는 분포를 NN의 invertible 함에서 얻는 것이 아니라, NN의 autoregressive 함을 통해 각 step의 평균과 분산을 얻는다.
        base distribution을 정보와 이전 스텝의 평균, 분산 정보를 활용하여 해당 step i의 x_i 값을 구한다.
      • Inverse Augoregressive Flow
        img
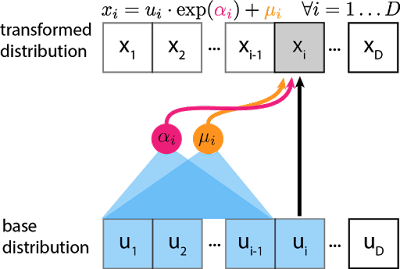
        위의 MAF 는 sampling 과정의 속도가 heavy해서, 평균과 분산을 얻는 것을 base distribution 에서 뽑아보자는 제안
  • Expectation & Variance
    • Expectation 은,, E[X] = sum(p_x*x) 임
    • Distrete Distribution
      • Bernoulli (Binary Distribution)
        • p(x) = p^x*(1-p)^(1-x)
      • Binomial
        • binary distribution 이 N번 수행되는 것
      • Negative Binomial
        • n 번의 failure 가 observable 할 때까지 몇 개의 1이 등장하는지 무한해질 수 있음
      • Poisson
        • event 의 발생 횟수가 궁금할 때
    • Continuous Distribution
      • Normal (CLT, useful in many domains) / Uniforam / Exponential
    • 어떤 distribution이 있는지 아는 것보다, 내가 사용하고자 하는 random variable 이 어떤 distribution에 mapping 되는지 인지하는 것이 더 중요함!
    • Variance
      • 평균으로부터 퍼져있는 정도
      • multiple variable 가 될 경우
        • joint distribution으로 표현할 수 있음
        • joint distribution 의 상대적으로 대조되는 개념은 marginal distribution!
          • marginal은 여러 다 변수 중 1,2개의 변수만을 고려하는 경우, 즉 그 1,2개의 변수만을 marginalized 시키는 경우이다.
      • Indepence
        • cdf, pdf, pmf 등에서 joint distribution이 각 random variable의 distribution으로 factorization 이 되면 독립이라고 말할 수 있음
    • Convariance
      • 두개 이상의 변수 사이의 퍼짐 정도. (variation의 extension)
      • 만약 두 변수가 independent 하다면, uncorrelated 하다고 말할 수 있음 (역은 성립 못함)
    • Correlation
      • Normalized version of covarriance 이다
      • corr[X,Y] = Cov[X,Y] / sqrt(Var(X), Var(Y)) (-1과 1 사이의 값)
    • Covariance Matrix
      • multiple variables 일 경우, Covariance 값을 각 변수 사이에 따라 matrix로 표현 가능
    • Multivariate Normal Distribution
      • Normal Distribution을 1변수에서 다변수로 자연스럽게 확장할 수 있음 scalar → vector
      • 매우 유용함
        • MLE(Maximum Likelihood Estimation) interpolation for least square
        • Gaussian Mixtutre Model
          • 여러가지의 Gaussian Dist component 들을 합성하는 방법론
        • Even in Bayesian DL (Gaussian Prior)
          • prior distribution을 가정하는 경우에도 많이 쓰임
      • 기억하기 !
        • joint distribution 이 normal 이면 marginal distribution도 normal 이다!
        • joint distribution 이 normal 이면 conditional distribution 도 normal이다!
          • 다소 복잡한(?) 값을 과정과 값을 가지지만, Schur complement 에 의해 Precision Matrix (Covariance의 Inverse Matrix) 의 값을 활용하여 계산하면, normal distribution 이 됨을 보일 수 있음

2 RULES! (Important)

  • conditinal probabiltiy
    • 일반적으로 딥러닝은, 기존의 데이터 X 가 주어질 때 , 새로운 보지 않은 데이터 X’ 가 나올 확률을 구하는 문제이다. 따라서 조건부 확률적인 부분이 중요하다.
      \(P_{Y|X}(y|x) = \frac{P_{X,Y}(x,y)}{P_X(x)}\)
    • 즉, conditional probability 는 “x가 이미 발생한 이후, joint distritbution 이 발생한 경우” 로 볼 수 있음
    • 참고
      • joint distribution P(X,Y)
        어떤 사건 X,Y가 동시에 일어나는 확률 분포
      • conditional distribution P(X|Y)
        사건 Y가 일어났을 때, 사건 X 가 일어날 확률 분포
      • marginal distribution P(X) or P(Y)
        joint distribution 이 다변수를 고려한다면, 그 중 하나의 변수를 고려할 때, “marginalized 되었다” 라고 표현한다.
        하나의 변수는 상수 취급하고, 하나의 변수만 취급하는 식으로 더 적은 변수들만 고려하는 경우
        (다변수에서 상대적으로 더 적은 변수를 고려할 때)
  • sum rule
    • P(x) = sum(P(x,y)) (y에대해 summation 할 때)
      • joint prob p(x,y) 를 y 또는 x 하나의 변수에 대해서 summation하면 marginal distribution을 얻을 수 있음.
    • continuous 한 경우는 integral 을 써서 보이면 됨.
  • product rule
    • joint distribution = conditional distribution * marginal distribution 이 됨.
    • P(X,Y)
      = P(Y|X) * P(X)
      = P(X|Y) * P(Y)
    • Example
      marginal prob P(Y_o)
      = P(Y_o, X_red) + P(Y_o, X_blue)
      = summation of {joint distribution}
      (joint dist. 은 product rule로 conditional dist. * marginal dist. 로 표현 가능)
      = P(Y_o|X_red) * P(X_red) + P(Y_o|X_blue) * P(X_blue)
      (각 joint distribution = product rule 로 값을 표현할 수 있음)
      so,
      = product rule_1 + product_rule_2
      (이 값들은 구할 수 있는 경우 有)
    • opinion) joint distribution을 conditional dist. 와 좀 더 적은 변수를 고려하는 marginal dist.로 분해할 수 있는 product rule이 꽤나 유용한 거 같음

Self 문답

  1. implicit 의 의미는?
    내가 이해한 바로는, y의 pdf는 얻을 수가 없다는 말이다. 왜냐하면, y로 가는 함수 f 자체가 direct 하게 distribution을 approximation 하려 하는 것인데, 이 f가 invertible 하지 않기 때문이다.

  2. 그래서 invertible한 tranformation 을 가지는 연구 흐름이 normalizing flow이다.
    affine transfomration, leakly ReLu 등 invertible 한 변환들을 활용하여, gradient 를 trackable하게 구하고, 기존 x 에서, y로 변환되는 부분들을 얻고자 하는 것이다.

  3. likelihood (가능도 즉, 어떤 결과 x가 관찰되었을 때, 그 결과가 나올 확률 분포 distribution이 얼마인지 예측하는 값)
    참고 링크 : https://jjangjjong.tistory.com/41

Reference

  • https://blog.evjang.com/2018/01/nf2.html
  • https://lilianweng.github.io/posts/2018-10-13-flow-models/
  • https://jjangjjong.tistory.com/41